shi转自:百度百科
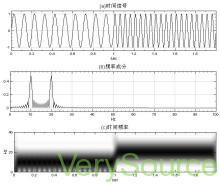
时频分析(JTFA)即时频联合域分析(Joint Time-Frequency Analysis)的简称,作为分析时变非平稳信号的有力工具,成为现代信号处理研究的一个热点,它作为一种新兴的信号处理方法,近年来受到越来越多的重视。时频分析方法提供了时间域与频率域的联合分布信息,清楚地描述了信号频率随时间变化的关系。
本文出自:https://baike.baidu.com/item/%E6%97%B6%E9%A2%91%E5%88%86%E6%9E%90
shi转自:百度百科

时频分析(JTFA)即时频联合域分析(Joint Time-Frequency Analysis)的简称,作为分析时变非平稳信号的有力工具,成为现代信号处理研究的一个热点,它作为一种新兴的信号处理方法,近年来受到越来越多的重视。时频分析方法提供了时间域与频率域的联合分布信息,清楚地描述了信号频率随时间变化的关系。
本文出自:https://baike.baidu.com/item/%E6%97%B6%E9%A2%91%E5%88%86%E6%9E%90
存档,转:百度百科
小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的,通过物理的直观和信号处理的实际经验的需要建立了反演公式,当时未能得到数学家的认可。正如1807年法国的热学工程师J.B.J.Fourier提出任一函数都能展开成三角函数的无穷级数的创新概念未能得到著名数学家J.L.Lagrange,P.S.Laplace以及A.M.Legendre的认可一样。幸运的是,早在七十年代,A.Calderon表示定理的发现、Hardy空间的原子分解和无条件基的深入研究为小波变换的诞生做了理论上的准备,而且J.O.Stromberg还构造了历史上非常类似于当前的小波基;1986年著名数学家Y.Meyer偶然构造出一个真正的小波基,并与S.Mallat合作建立了构造小波基的统一方法加多尺度分析之后,小波分析才开始蓬勃发展起来,其中比利时女数学家I.Daubechies撰写的《小波十讲(Ten Lectures on Wavelets)》对小波的普及起了重要的推动作用。它与Fourier变换、窗口Fourier变换(Gabor变换)相比,这是一个时间和频率的局域变换,因而能有效的从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析(Multiscale Analysis),解决了Fourier变换不能解决的许多困难问题,从而小波变化被誉为“数学显微镜”,它是调和分析发展史上里程碑式的进展。 [1]
本文出自:https://baike.baidu.com/item/%E5%B0%8F%E6%B3%A2%E5%88%86%E6%9E%90/1504577?fr=aladdin