室内数据处理上机实习使用的是美国科罗拉多矿院开发的CWP/SU软件，该软件具有非常强大的地震勘探数据处理功能，包括：制作地震合成记录，对各种噪声的处理，动、静校正功能，叠加和偏移等。本次室内数据处理上机实习的具体内容：
本文为原创文章，转载请注明出处！
EI当n＝1时，Bezier曲线的控制多边形有二个控制点P0和P1，Bezier曲线是一次多项式。
当n＝2时，Bezier曲线的控制多边形有三个控制点P0、P1和P2，Bezier曲线是二次多项式。
当n＝3时，Bezier曲线的控制多边形有四个控制点P0、P1、P2和P3，Bezier曲线是三次多项式。
在区间〔0,1〕范围内，每个基函数均不为零，说明不能使用控制多边形对曲线的形状进行局部调整，如果要改变某一控制点位置，整条曲线都将受到影响。
根据以上性质知道，Bezier曲线是拟合曲线，在控制多边形的第一个顶点和最后一个顶点处进行插值，其形状直接受其余控制点的影响。
（1）曲线过控制多边形的起始点和终止点。
（2）曲线起始点处的一阶导数是通过第一个控制点和第二个控制点之间的矢量来定义；曲线终止点处的一阶导数是通过最后一个控制点和倒数第二个控制点之间的矢量来定义。
（3）曲线在起始点的二阶导数依赖于起始的3个控制点；曲线在终止点的二阶导数依赖于最后的3个控制点。
本文为原创文章，转载请注明出处！
远探测声波的远探测技术分为单极纵波法和偶极横波法两种。单极纵波法，就是利用井中
单极子声源向井外地层辐射纵波，然后记录从井旁地质体反射回来的纵波，通过反射纵
波所携带的信息确定该地质反射体的位置 。由于单极纵波法所采用的激发声源是无方
向性的单极声源，因而该方法的处理结果只是地层三维空间中界面的二维图像，不包含
反射体的方位信息。而且，单极声源的工作频率一般在 10kHz 左右，频率较高会造成较
大的波幅衰减，从而导致其探测范围有限，单极纵波法的探测范围约为井旁数米到十数
米
本文为原创文章，转载请注明出处！
冈萨雷斯书中第三章和第四章分别讲了空间滤波和频率域滤波，维纳滤波放在了第五章图像复原和重建。第五章其实就是滤波的应用，因为图像有退化，所以才要复原，而要想复原，必须要搞清楚图像退化的过程。一幅图像从镜头捕捉到传输，存储都会产生各种各样的畸变，这些过程统称为退化过程。可以发现，图像退化是相对于两幅图像而言的，一幅是原图，一幅是退化后的图像，图像复原的目的是将退化后的图像变换到尽量接近原图的过程，即退化的逆过程。尽量接近原图就是我们的指标，所以图像复原是一个客观的过程，而图像增强是一个主观的过程，输出图像的指标是人类视觉的接收程度。
数学上，我们把退化过程分成两部分，一个是退化函数H，一个是加性噪声。所以频率域退化模型如下式：
本文为原创文章，转载请注明出处！
1、水平界面时距曲线（埋深100米）
假设地下有一个水平地质界面，埋藏深度100m，地层是均匀的各向同性介质，地震波纵波传播速度为1500m/s，请编制C或Matlab程序，绘制出中点放炮共炮点的反射波、直达波和折射波时距曲线（参考附图1）。Matlab程序编制中，炮检距：-500m~500m，间距10m；临界角取35°。
假设上述水平界面模型中界面埋藏深度变为1000m，上述时距曲线有何变化，绘出相应图形，并从理论上加以分析；
假设地下有一个倾斜界面，地层倾角为20°，地层是均匀的各向同性介质，地震波纵波传播速度为1500m/s，请编制C或Matlab程序，绘制出端点放炮共炮点的反射波、直达波和折射波时距曲线（参考附图2）。C或Matlab程序编制中，炮点处界面的法向深度为100m；炮检距：-500m~500m，间距10m；临界角取35°。
假设地下有一个绕射点，埋藏深度为1000m，绕射点以上地震波传播速度为1500m/s，编制C或Matlab程序计算并绘制出绕射波时距曲线图。C或Matlab程序编制中，炮检距：-1000m~2000m，间距20m；绕射点在地面的投影点距离炮点200m（参考附图
本文为原创文章，转载请注明出处！
著名的鸡尾酒问题，n个人同时讲话，n个麦克风接收，采集n组叠加的声音数据，每组数据包括m个元素。问题：如何恢复n个人的讲话声音？
设原始信号为S，叠加的线性关系为A，接收的信号为X，则有
X=AS
其中，n个麦克风接收信号X(X1,X2,…Xn)；源信号S(S1,S2,…Sn)。Xi,Si均为列矢量。
X和S的信号长度相同
A为混淆矩阵/混合矩阵，根据线性方程组的关系。S、X均为n行m列，则A只有为n行n列才能满足要求。
x11=A11.S11+A12.S21+…+A1n.Sn1 (A的某a行与S某b列相乘，得到Xab值)
x12=A11.S12+A12.S22+…+A1n.Sn2
x1m=A11.S1m+A12.S2m+…+A1n.Snm
x22=A21.S12+A22.S22+…+A2n.Sn2
因此 ，设
若要使求解矩阵最大程度上逼近S，这实际上就是个优化过程，只需要满足解混合矩阵是最佳估计A的逆矩阵就好。ICA是盲源信号分离。
ICA算法的研究可分为基于信息论准则的迭代估计方法和基于统计学的代数方法两大类，从原理上来说，它们都是利用了源信号的独立性和非高斯性。
基于信息论的方法，各国学者从最大熵、最小互信息、最大似然和负熵最大化等角度提出了一系列估计算法。如FastICA算法, Infomax算法，最大似然估计算法等。
基于统计学的方法，主要有二阶累积量、四阶累积量等高阶累积量方法。
本文为原创文章，转载请注明出处！
傅立叶变换有一个缺点：它不具有时间局部性。这点可从傅立叶正/反变换的公式中看出，
， （2-1）
式（2-1）中的积分区间为，即整个时间轴或频率轴。因此要想获取信号的频域信息必须知道信号在时域的全部分布；同理，要想恢复信号的时域波形，也必须知道信号频域的全部信息。信号进行傅立叶变换后得到频谱能够表明信号所含的频率成分，但无法表明该频率发生的时刻，这使得傅立叶变换在分析非平稳信号时具有局限性。
可通过下例具体说明：图1-1为一在不同时间内频率不同的正弦信号的时域波形和信号的频谱图，该信号在内为2,内为4, 内为8,内为16。图1-2为另一信号的时域波形和信号的频谱图，该信号在内为4个正弦信号的叠加，正弦信号的频率分别为2，4，8，16。
图1-1不同时间段内所含频率成分不同
图1-2任意时间段含有4种频率成分
从图1-1和图1-2可以看出，两信号在时域相差很大，但在频域上差别并不是非常明显，均在2，4，8，16处能量较强，而在其他频率处能量较低。仅从两者的频谱图，我们无法判断出信号的时域波形。
对于上例所示的简单信号，傅立叶变换都具有一定的局限性，更别说对于一些更为一般的信号了，如我们想分析一些音乐片段所包含的频率时，对信号做了傅立叶变换，得到了频谱，但从频谱上我们并不能判断出高频出现在什么时刻，低频出现在什么时刻，得到的频谱并不明显，在这种情况下，傅立叶变换的实际意义不大。
加窗傅立叶变换（WFT：Windowed Fourier Transform）也称短时傅立叶（STFT: Short Time Fourier Transform）或窗口傅立叶变换，是用一个在时间上有一定宽度的窗函数在时间轴上平移，并和待分析的信号相乘，然后再用傅立叶变换对相乘信号进行分析，得到该时刻附近对应信号的频谱。
WFT的实现过程如下：
（1-2） 实现过程也可用图1-3所示：信号与窗相乘（仅在内有非零值），得到一个仅在区间内有值的函数，对做FT，得到一个反映信号在区间内频谱的函数。沿时间轴做上述变换便可得到信号的WFT。
图1-3 加窗傅立叶变换示意图
若选为矩形窗分别对图1-1和图1-2中两信号进行WFT，所得结果如图1-4和图1-5所示：
(a)窗函数 (b)加窗傅立叶变换 (c)加窗傅立叶变换
结果的幅度图 结果的俯视图
图1-4加窗傅立叶变换（图2-1中信号）
(a)窗函数 (b)加窗傅立叶变换 (c)加窗傅立叶变换
结果的幅度图 结果的俯视图
图1-5加窗傅立叶变换（图1-2中信号）
图1-4和图1-5中(a)图为窗函数的波形，(b)图为WFT结果的幅度图（两坐标分别为时间和频率），(c)图为WFT结果的俯视图。
从图1-4可以看出:4个不同时间段内，信号的能量在频域的分布不同：时间内信号能量集中在2附近，时间内信号能量集中在4附近，时间内信号能量集中在8附近，时间内信号能量集中在16附近。
从图1-5可以看出:在的任意时间段内，信号都主要有4个频率成分，分别为2，4，8，16。
图1-4和图1-5的结果可以从直观上区分这两种信号，从而体现了WFT的优势。
（1-3）
式（1-3）即为WFT的重构公式[4]。
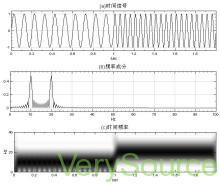
图1-6为一鸟声信号的WFT及其重构的波形和重构的误差，该信号在内，频率从0线性增加至8。
图1-6 鸟声信号的WFT结果和重构
图1-6的上方左图为鸟声信号的波形，上方右图为归一化的窗函数，中间左图为WFT结果的幅度图，中间右图为WFT的时频图，下方左图为重构出来的鸟声信号，下方右图为信号的重构误差。
可以看出，在内信号的频率是线性上升的，重构的鸟声信号波形与原信号在肉眼可观察范围内完全一样，重构误差的模取对数后可以看出重构误差为~数量级，达到计算机的计算误差精度，说明WFT可以进行无差重构，即重构公式（1-3）是正确的。
仍以图1-6中的鸟声信号为例通过改变窗的宽度，观察信号进行WFT后时频图的变化。
图1-7是同一个窗函数（矩形窗）在不同宽度时信号WFT的时频图。图1-7的（a），（b），（c），（d），（e），（f）6个子图窗的宽度依次为2s，4s，8s，1.5s，1s，0.5s。从图1-7可以看出：从（a）~（c），随着窗宽度的增加，时频图中频谱逐渐变“宽”，显示的效果逐渐变差；从（d）~（f），随着窗宽度的减小，频谱也是逐渐变“宽”，显示的效果也逐渐变差。
可以看出，只有窗的宽的在一定的范围内时，WFT才能获得较好的显示效果，窗过窄或过宽时频图的显示效果都将变差。
(a) (b) (c)
(d) (e) (f)
图1-7加窗傅立叶变换时频图(—宽度)
上述现象可以用Heisenberg测不准原则解释：
Heisenberg’s uncertainty principle:
设窗函数，且满足，则：
（1-4） 式中：为窗函数的时域宽度（单位为），表征了窗函数的时间分辨率，越小表明时间分辨率越高；为窗函数的频域宽度（单位为），表征了窗函数的频率分辨率，越小表明频率分辨率越高。
Heisenberg测不准原则表明了窗函数时域宽度和频域宽度之积不可能小于某一个定值，即限制了窗函数不可能同时具有很高的时间分辨率和频率分辨率。
图1-7中从（a）~（c）窗的宽度逐渐增加，频域的宽度逐渐减小，频率分辨率逐渐增强，时频图中边界处变清晰了。频谱逐渐变“粗”是因为窗逐渐变宽，时间分辨率逐渐变差。进行WFT时某一时刻做傅立叶变换时，该时刻对应的频率成分应包括以时刻为中心的一段时间内该信号的频率成分。以图1-7(c)为例，窗的宽度为8s，且为对称的，所以做WFT时某时刻的频率组成应包括时间段内信号的频率成分。同理，某时刻的频率成分也会出现在时间内，即某一时刻的频率成分会持续8s（窗的宽度）。
图1-7中从（d）~（f）窗的宽度逐渐减小，时间分辨率逐渐提高，但频率宽度逐渐变宽，频率分辨率逐渐减弱，频谱逐渐变“宽”。边界处变模糊了，有旁瓣出现，且窗的宽度越小，旁瓣现象越明显。
图1-7说明了窗宽度的重要性，在分析信号的时频谱时应兼顾窗函数的时间分辨率和频率分辨率，选择合适的宽度，以获得较高的时频联合分辨率。
本文为原创文章，转载请注明出处！
shi转自：百度百科
时频分析（JTFA）即时频联合域分析（Joint Time-Frequency Analysis）的简称，作为分析时变非平稳信号的有力工具，成为现代信号处理研究的一个热点，它作为一种新兴的信号处理方法，近年来受到越来越多的重视。时频分析方法提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。
本文出自：https://baike.baidu.com/item/%E6%97%B6%E9%A2%91%E5%88%86%E6%9E%90
存档，转：百度百科
小波变换的概念是由法国从事石油信号处理的工程师J.Morlet在1974年首先提出的，通过物理的直观和信号处理的实际经验的需要建立了反演公式，当时未能得到数学家的认可。正如1807年法国的热学工程师J.B.J.Fourier提出任一函数都能展开成三角函数的无穷级数的创新概念未能得到著名数学家J.L.Lagrange，P.S.Laplace以及A.M.Legendre的认可一样。幸运的是，早在七十年代，A.Calderon表示定理的发现、Hardy空间的原子分解和无条件基的深入研究为小波变换的诞生做了理论上的准备，而且J.O.Stromberg还构造了历史上非常类似于当前的小波基；1986年著名数学家Y.Meyer偶然构造出一个真正的小波基，并与S.Mallat合作建立了构造小波基的统一方法加多尺度分析之后，小波分析才开始蓬勃发展起来，其中比利时女数学家I.Daubechies撰写的《小波十讲（Ten Lectures on Wavelets）》对小波的普及起了重要的推动作用。它与Fourier变换、窗口Fourier变换（Gabor变换）相比，这是一个时间和频率的局域变换，因而能有效的从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析（Multiscale Analysis），解决了Fourier变换不能解决的许多困难问题，从而小波变化被誉为“数学显微镜”，它是调和分析发展史上里程碑式的进展。 [1]
本文出自：https://baike.baidu.com/item/%E5%B0%8F%E6%B3%A2%E5%88%86%E6%9E%90/1504577?fr=aladdin