先产生了一个正弦信号便于分解,显示其波形和频谱图便于对照。
clear;clc;
%% 产生原始信号
f1=5; % 信号1的频率
f2=2; % 信号2的频率
f3=10; % 信号3的频率
fs=30; % 采样率
N=fs*60;
t = 0 : 1/fs : (N-1)/fs;
y1=5*sin(2*pi*f1*t)+10*sin(2*pi*f2*t)+8*sin(2*pi*f3*t);
figure(1);subplot(2,1,1);plot(y1,'r');
%% 画出原信号的频率谱
n=0:N-1;
f=n*fs/N;
y=fft(y1,N);
mag=abs(y)*2/N;
subplot(2,1,2);
plot(f(1:N/2),mag(1:N/2));
%% 画出EMD分解的IMF值的图像
% [imf,residual,info] = emd(y1,'Interpolation','pchip');
emd(y1,'Interpolation','pchip');
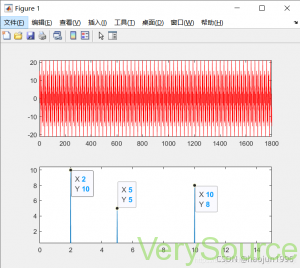
原始信号的波形及频谱图如图所示:
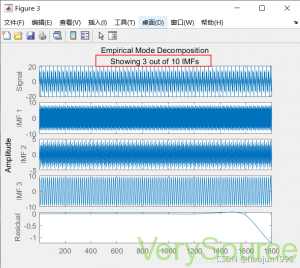
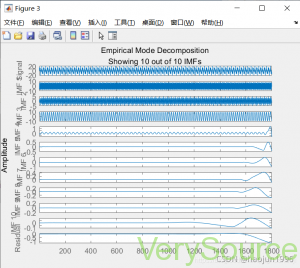
EMD函数画出的图像如图所示:(只自动显示了3个IMF图像)
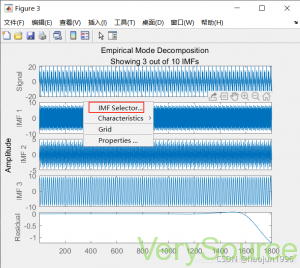
在空白位置单击右键可以选择显示剩下的IMF值。
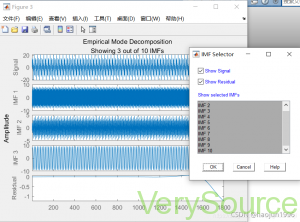
按OK后即可同时显示所有IMF的图像。
同时显示波形和频谱图
对上面的代码需要简单的修改,该方法需要知道每个IMF分解出的值,并通过FFT变换为频域中画图。
[imf,residual,info] = emd(y1,'Interpolation','pchip');
for i= 1:size(imf,2)
subplot(size(imf,2),2,2*i-1);plot(imf(:,i));
subplot(size(imf,2),2,2*i);
y1=fft(imf(:,i),N);
mag=abs(y1)*2/N;
f=n*fs/N;
plot(f(1:N/2),mag(1:N/2));
end
运行结果如下图所示:
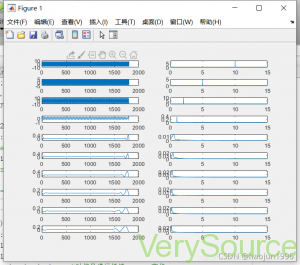
[imf,residual,info] =emd(y1,‘Interpolation’,‘pchip’);该式子可获取到EMD分解的结果,即IMF值及残差值等参数,在后续可以通过for循环画出对应的波形和频谱图。
可以通过matlab右侧的变量区看分解出来的IMF是横着的还是竖着的格式。
在EMD函数中可以通过添加参数来增多分解的IMF值,在matlab的输入参数部分可以找到详细介绍,同时也推荐一位up主的学习视频。
可以通过[imf,residual,info] = emd(y1,‘Interpolation’,‘pchip’,“SiftRelativeTolerance”,0.02);个人理解的是修改后面的参数值会分解得更细致,本来默认的0.2可能会使幅度相近的两个信号在一个IMF中,改小可以识别到这样的情况会减小混叠情况。
推荐学习视频https://www.bilibili.com/video/BV1Tk4y1r7h1
本文出自:https://blog.csdn.net/haojun1996/article/details/120946887